Euler spirals and road design

A French Curve

For a few years we used to give out to all incoming students wooden French curves. These were laser cut by college technicians during the summer recess and were included in the fresher's pack. However I never saw any students using them and I have noticed that they are no longer given out. Perhaps what was missing in the pack was any information as to what French curves were used for and why. When I was a technical draftsman they were essential if you were to draw smooth curves and in particular if you were to develop a curve that gradually moved away from a straight line, in such a way that there seemed to be a smooth inevitability to it. This was because French Curves were based on the Euler spiral, a curve that has a curvature that changes linearly with its curve length. (Euler spirals are also called spiros, clothoids, or Cornu spirals) 
There are lots of applications for Euler spirals, usually as transition curves and you tend to meet with them in real life situations such as driving on the roads or riding in trains. Both being situations where a sudden tight curve would be very dangerous.

I have posted on mathematical shape before and will continue to do so whenever I come across what I think are interesting facts about certain types of geometries, topologies or patterns and this particular property of curve, one that has a curvature that begins with zero at the straight section (the tangent) and increases linearly with its curve length, is visually reminiscent of the Bezier Curve that we looked at a while ago.

On railroads during the 19th century, as speeds increased, the need for a track curve with gradually increasing curvature became apparent. Euler spiral forms were seen as the answer to these increasing speeds and by the time these forms were formalised for the railways by being published by Higgins in 1922, several different mathematicians had laid claim to their properties, including the Italian mathematician Ernesto Cesàro who gave the name ”Clothoid” to the curve in response to its double spiral shape, naming it after Clotho one of the three Fates who spun the thread of human life, by winding it around the spindle.

The Euler or Clothoid curve

Humans were soon to develop other fast forms of transport and automobiles would need roads and when roads were linked up, if the traffic was not to come to a complete standstill, they would need roundabouts. 
Engineers developed a range of forms, each one based on the Euler curve, to visualise their road designs and these designs when isolated from their function are rather beautiful images. The evolution of interchanges and the emergence of the plated road interchange is particularly interesting. 

The first complex roundabout system to use Euler curves was the cloverleaf interchange.

Cloverleaf Interchange

First patented by Arthur Hale in 1916, the smooth curved slip roads allowed traffic to leave and merge with fast highways with minimum speed changes. However in the USA in particular traffic density continued to increase and more complex forms were needed. 

Stack interchanges were then developed and these had a much higher capacity when it came to dealing with high volumes of traffic. However they are very expensive to construct due to the complex nature of their interconnections.

The stack interchange

The turbine or whirlpool interchange was the next development, needing fewer levels than a stack interchange and therefore being cheaper to build. 

The turbine interchange

The latest development is the Pinavia road interchange, a form that eliminates the central cross layering of construction, so being even cheaper. 

Pinavia road interchange

All of these complex geometries are in use and many of you will have driven through them without realising what they looked like from above. I love their forms and in the same way that complex geometry lies at the centre of Islamic design, I would suggest that it is geometry that gives meaning to our present day urban infrastructure. We tend to forget the work of engineers, people that use their knowledge of geometry and mathematical form to ensure that our built environment is fit for purpose. I would suggest that their use of geometry serves a higher purpose than just function and that engineers are also aware of aesthetic values and embed them into their designs. 

The artist Carol Rhodes was fascinated by these forms, in particular how they created formal divisions across the landscape. Rhodes' paintings are fascinating as they sit in a pictorial space between map making and landscape painting.

Carol Rhodes: Study for a painting

Carol Rhodes, River, Roads (2013) 

I have also looked at principles of road roundabout design before. For instance Piet Hein used the shape of the super-elipse to design roundabouts, which was his way of calming traffic and also allowing for a smooth transition from cars moving in straight lines into tight curves. A range of related mathematical shapes of interest can be found here. 

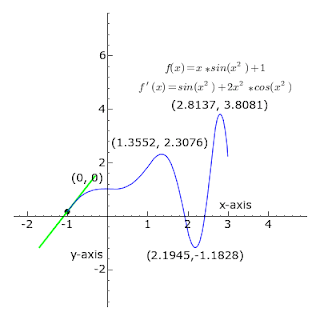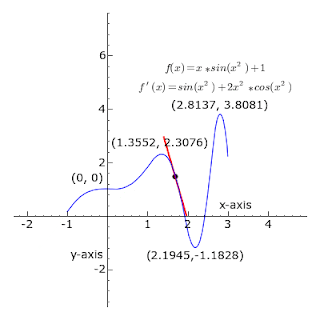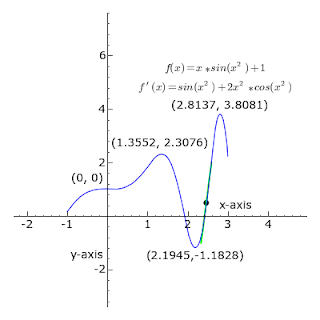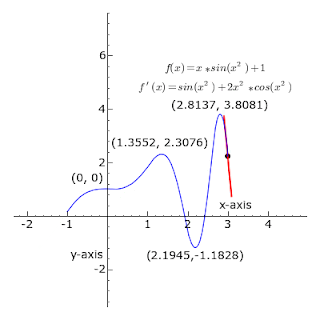
Whether we are looking at Bezier curves or Euler curves the relationship between straight lines and circles is expressed via an understanding of tangents. More precisely, a straight line is said to be a tangent of a curve y = f (x) at a point x = c on the curve if the line passes through the point (c, f (c)) on the curve and has slope f '(c) where f ' is the derivative of f. 

As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. 

There are of course many other uses for these curves that are derived from the various ways that tangents can be developed, but I think it is interesting how many have been used to develop our fascination with transport, whether it is designing the smooth shapes of the cars themselves, (Bezier curves) or the roads that they travel on. 

However there is another aspect to Euler curves and that is that when visualising 3D shapes that have been formed by hand, the aesthetic of rightness that I have also discussed before,  comes into its own. These curves give much better predicted results when trying to visualise what's missing in old broken pottery. Perhaps at a deeper level we intuitively understand these types of forms and make them because our own hands and arms are attached to fixed lever points and operate within the limits of similar curves when trying to make things. 

Using Euler curves to predict what the gaps represent in a broken statue

See also: Abstraction, metaphor, mathematics and creation 

Hogarth's line of beauty and other aspects of flowing lines